DCモータのモデリング
(ブラシ付き)DCモータの動きをspice上で再現するために,DCモータの等価回路を導く.DCモータは,比較的安価・小型なモータで,入手が容易であるため,電池があれば動きを目で見て確認することができる.モータを電池につなぐともちろんモータが回り始めるが,とくにプロペラなどをモータに取り付けた場合,それがモータの回転を妨げる要素(これを負荷とよぶ)となり,電池をつないでしばらく時間が経過してからモータの回転速度(角速度とよぶ)が一定となることが目視によって確認できるだろう.「しばらく時間が経過してから回転速度が一定となる」という状況は,一般に「遅れ」ということばで表現される.
たとえば,扇風機を考えてみよう.扇風機の羽の軸にはモータが接続されている(大抵の場合,DCモータとは異なるタイプのモータが用いられる).扇風機には,「弱」「中」「強」のように風量を調節するスイッチ類が備えられている.我々はこのスイッチを押すことによって,望みの風量を選択できるわけであるが,その仕組はどうなっているのだろうか.もちろん何らかの制御を使ってうまく仕組まれているのである.
そこでまずはうまく仕組まれていない状況をよく観察することから始めよう.それにはDCモータの動きを数式で表すのが有効である.DCモータの動きは,次の方程式によって近似的に表現される.
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
これらの式に含まれる文字のうち,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() は時間の関数を表す変数である.
は時間の関数を表す変数である.
 : モータ端子間の電圧[V]. モータ端子に電池などの電気エネルギーを供給する源を接続したときの端子間電圧.この電圧は,モーターが回り始めるきっかけとなるので入力電圧,あるいは単に入力とよばれる.符号は二つの端子を見ながら自分で決めればよい.
: モータ端子間の電圧[V]. モータ端子に電池などの電気エネルギーを供給する源を接続したときの端子間電圧.この電圧は,モーターが回り始めるきっかけとなるので入力電圧,あるいは単に入力とよばれる.符号は二つの端子を見ながら自分で決めればよい. : モータ端子間の電流[A]. モータ端子に電池などを接続した状況を考えた場合,
: モータ端子間の電流[A]. モータ端子に電池などを接続した状況を考えた場合, もまたモータが回り始めるきっかけになるので,
もまたモータが回り始めるきっかけになるので, 同様,入力電流とよんでもよい.しかし通常は負荷にかかわらず一定の電圧を出す独立電圧源に近い電源を接続することが多いので,
同様,入力電流とよんでもよい.しかし通常は負荷にかかわらず一定の電圧を出す独立電圧源に近い電源を接続することが多いので, は従属的に決まる物理量と考える.この場合
は従属的に決まる物理量と考える.この場合 は入力電流とよぶべきではない.符号は二つの端子を見ながら自分で決めればよい.
は入力電流とよぶべきではない.符号は二つの端子を見ながら自分で決めればよい. : モータの角速度[rad/s]. モータから出ている軸の,単位時間あたりの角度変化のこと.符号はモータの筐体に対して自分で決めればよい.
: モータの角速度[rad/s]. モータから出ている軸の,単位時間あたりの角度変化のこと.符号はモータの筐体に対して自分で決めればよい. : モータ端子間に生じる逆起電力[V]. モータが一定の角速度
: モータ端子間に生じる逆起電力[V]. モータが一定の角速度 で回っていると仮定すると,モータ端子間を結ぶ導線が磁界中で一定の速度で運動することになり,導線に起電力が生じるが,この起電力のこと.この現象はフレミングの右手の法則によって説明できる.(1)からわかるようにモータ端子間電圧
で回っていると仮定すると,モータ端子間を結ぶ導線が磁界中で一定の速度で運動することになり,導線に起電力が生じるが,この起電力のこと.この現象はフレミングの右手の法則によって説明できる.(1)からわかるようにモータ端子間電圧 とは異なる.
とは異なる. : モータ端子間に電流
: モータ端子間に電流 を流すことによって発生するトルク[N
を流すことによって発生するトルク[N m]. トルクとは,物理学でいうところの力のモーメント.なぜそのようなトルクが発生するかはフレミングの左手の法則によって説明できる.
m]. トルクとは,物理学でいうところの力のモーメント.なぜそのようなトルクが発生するかはフレミングの左手の法則によって説明できる.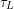 : モータの軸には,回したいもの,たとえば扇風機なら羽をつけて使用する.このモータによって回されるものを負荷とよぶが,負荷はモータから与えられるトルクによって回ることになる.そのトルクを
: モータの軸には,回したいもの,たとえば扇風機なら羽をつけて使用する.このモータによって回されるものを負荷とよぶが,負荷はモータから与えられるトルクによって回ることになる.そのトルクを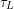 と表している.モータ側からみれば,作用・反作用の法則によってマイナスをつけた
と表している.モータ側からみれば,作用・反作用の法則によってマイナスをつけた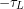 がモータに働くことになる(3).
がモータに働くことになる(3).
式中に含まれる他の文字はすべて定数である.これらの定数はモータ自体がもつパラメータであり,どれも正の実数である.それらの一部はモータを作っているメーカーによって提供されていることもある.
(1)-(4)を電気回路に置き換えてみよう.そのためには力学的な変数やそれに伴う物理量を等価な電気的な量に置き換えなければならない.
そこで,新しい変数として負荷電流![]() [A]を
[A]を
(5) ![]()
と定義する.またこれに伴って新しい定数
(6) ![]()
を導入しておく.(5), (6)のもとで(1)-(4)を書き換えると次のようになる.
(7) ![]()
(8) ![]()
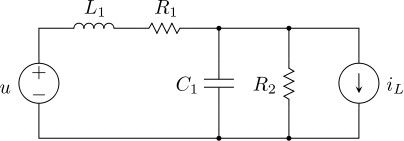
これらの式に相当する電気回路を描くことができる.(7), (8)をそれぞれキルヒホッフの電圧則,電流則とみなせば次のようなモータの等価回路が得られる.
 SPICEで制御工学を
SPICEで制御工学を